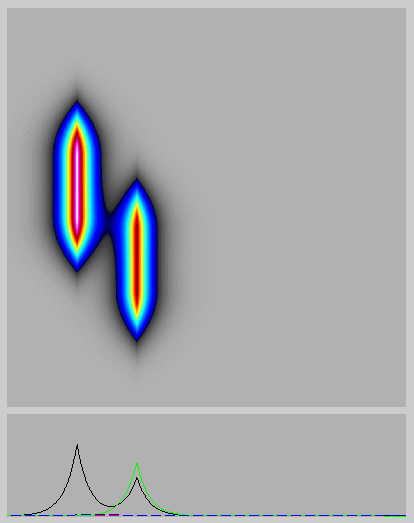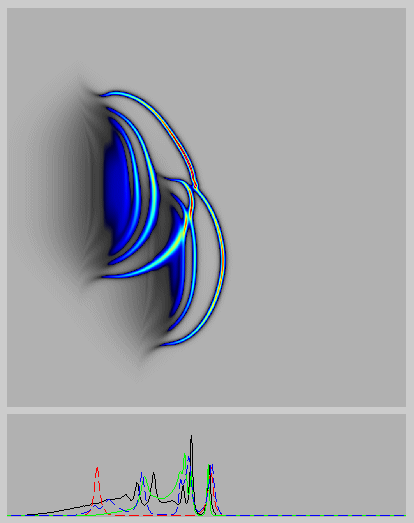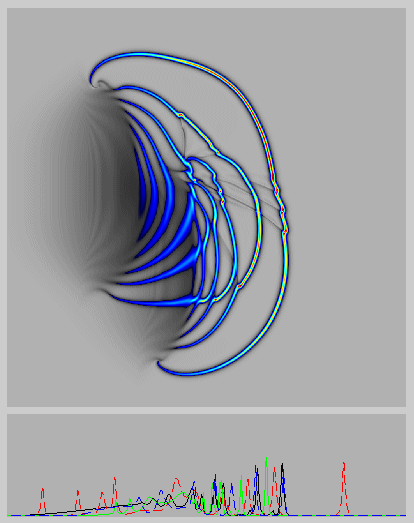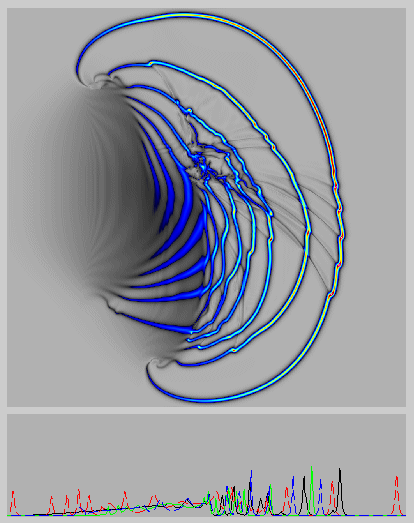
The figure/animation shows numerical simulations of the evolution and interaction of singular solutions of the EPDiff equation from DD Holm and MF Staley (submitted). EPDiff is short for Euler-Poincare equation on the diffeomorphisms. EPDiff may be derived as a shallow water equation, which applies to the propagation and interaction of nonlinear internal waves. The surface effects of these internal waves are observed in Nature, for example, on the Ocean surface, such as at the Strait of Gibralter shown in the figure above. In the animation, two straight segments are initialized moving rightward. The one behind has twice the speed of the one ahead, and the two segments are offset in the vertical direction. The segments each break into curved strips of a certain width and these undergo overtaking collisions. The segments retain their integrity as they expand until the overtaking collision occurs. Upon overtaking a slower segment, the faster segment transfers its momentum to the slower one ahead and a remarkable ``reconnection'' or ``melding'' of the segments may occur. This reconnection also shows rapid transverse stretching in which ``hot spots'' of velocity arise and then spread out along the wave front. In addition, the figures show low amplitude ``peakon wisps.'' The peakon wisps each connect the endpoint of an earlier reconnection to a point (usually to a hotspot) on the leading peakon segment. These wisps apparently provide the ``memory'' of the previous reconnection, which is required for the evolution to remain reversible. Its reversibility affirms the nondissipative (Hamiltonian) nature of the reconnection process.